前回の記事の補足とか

前回、ある命題A,Bを用いて

"A ⇒ B" という命題が定義され、

それが "￢A∨B" という命題の真偽と一致することを説明しました。

真偽が一致する、いわば2つの命題が同値（論理同値）であることを

"P ≡ Q" や "P ⇔ Q" などといった記号で表します。

つまり "A ⇒ B ≡ ￢A∨B"・・・① と書けるわけです。

この関係を覚えるためのいい例文があったので紹介します。それは、

「動いたら殺すぞ！」

「動くな、さもないと殺すぞ！」

この２つです。どちらも同じ事を言ってますよね？

「動く」という動作をAとし、「殺す」という動作をBとします。

すると、

「AするならばBするぞ！」・・・"A ⇒ B"

「Aするな（￢A）、さもないと（∨）Bするぞ！」・・・"￢A∨B"

①の関係と一致しますね。


ただ、この覚え方はうちの学校の生徒にとってはあの事件を彷彿とさせるとして不評だという噂です（


もう一つ補足というか自分が考えたことについてなんですが

100年ほど前の数学者は命題A,Bについて「AならばB」を

"A⊃B"と表記しました。

A,Bがある集合ならば「AならばB」は

"A⊂B"と表記しますよね？

これらの記号「⊂,⊃」は論理学と集合論では意味が違うものらしいですが

同じような記号を用いるということは何か意味があると考えるのが普通じゃないでしょうか。


集合においての「AならばB」をベン図で示すとこんな感じです。
















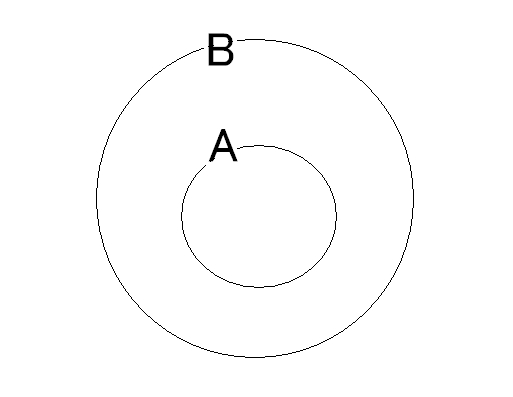
Aという集合はBという集合の部分集合「A⊂B」という関係になっています。

定義からしてこれはOK。


では論理においてある命題a,bに対しての「aならばb」はどうでしょうか。

抽象的な話になりますが仮にa,bが真の場合にその命題が示す概念の集合をA,Bとします。

もしそのとき「aならばb」、つまり「aが真ならばbは真」が "A⊂B" と表せたらどうなるでしょう。

まず、aが真であるとしてそれが示す概念、集合Aの内部を塗りつぶしてみます。
















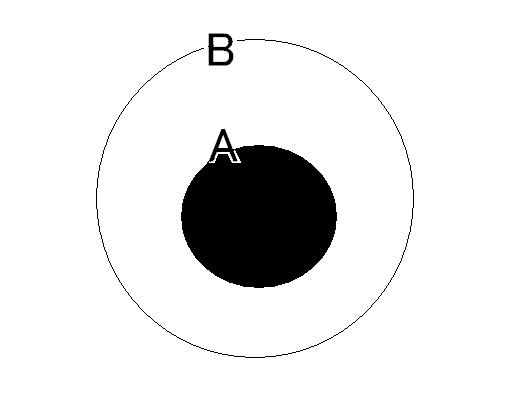
ではこのとき「bは真」となっているでしょうか？

「bは真」が示す概念の集合Bの内部は全て塗りつぶされていません。

つまりこの図の関係"A⊂B"では「aが真ならばbは真」がいえないのです。


では、"A⊃B"の関係を表すベン図を用いてみましょう。

Aの内部を塗りつぶすと
















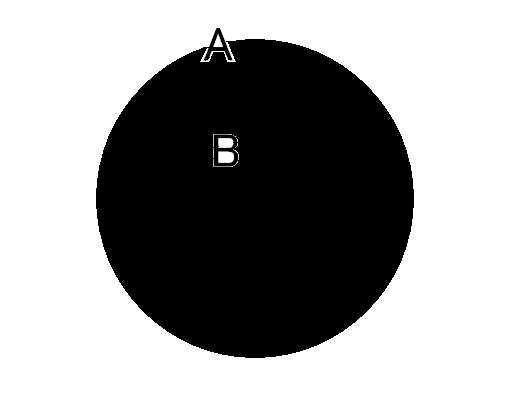
Bの内部も塗りつぶされて「aならばb」が成り立っているのが分かるでしょうか？

だから昔、ある命題a,bについての「aならばbである」は "a⊃b" という表記がされていたことも

納得できるのではないかと僕は考えます。

この関係を「aはbを含意する」ともいうことも自然なことではないですかね？


追記：
さらに補足的な話ですが

「アンパンがパンならば1+1=2である」

「1=2ならば人間は生き物ではない」

などの命題も真となります。

「AならばBである」の命題A,Bが全く関係のない事柄であっても

あくまで論理学における含意というものはのA,Bの真偽によって決まるものです。


今回はこれで！

では。

2012/03/24 (Sat) 数学 Comment(0)