更新は不定期でだいたい0時ぐらい。
×
[PR]上記の広告は3ヶ月以上新規記事投稿のないブログに表示されています。新しい記事を書く事で広告が消えます。
みなさん判別式というと二次方程式の判別式D=b^2-4acをまず思い浮かべると思います。
でもこれを解の公式から導き出すことを学校で教えられ、なんとなく使っている人も多いでしょう。
今回は判別式についてお話しします。
ではまず説明に使う用語と記号について紹介します。
めんどうな場合は読み飛ばして(続き)に飛んで下さい。
一つ目は「根」について

「解」によく似てますね。でも解とは少し違います。
「解」とはあくまでf(x)=0を満たすxの値のことです。
同じものが2つあればそれをまとめて一つとして考えます。
例えば、(x-1)^2=0の「解」は一つですが「根」は2つと考えます。
でも今回は、同じものだとして「解」と読みかえてもらっても構いません。
2つ目に総乗記号についてです。総乗記号Πは次のように定義されます。
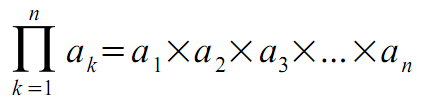
要するにΣ(シグマ)の掛け算バージョンと思えばすぐ理解できるでしょう。
でもこれを解の公式から導き出すことを学校で教えられ、なんとなく使っている人も多いでしょう。
今回は判別式についてお話しします。
ではまず説明に使う用語と記号について紹介します。
めんどうな場合は読み飛ばして(続き)に飛んで下さい。
一つ目は「根」について
「解」によく似てますね。でも解とは少し違います。
「解」とはあくまでf(x)=0を満たすxの値のことです。
同じものが2つあればそれをまとめて一つとして考えます。
例えば、(x-1)^2=0の「解」は一つですが「根」は2つと考えます。
でも今回は、同じものだとして「解」と読みかえてもらっても構いません。
2つ目に総乗記号についてです。総乗記号Πは次のように定義されます。
要するにΣ(シグマ)の掛け算バージョンと思えばすぐ理解できるでしょう。
------------------------------------------------------------------------
(続き)
ではここからが本題です。
判別式とはその多項式に重根(重複した根)が存在するかどうか確かめるための式です。
重根が存在すれば判別式は0となります。
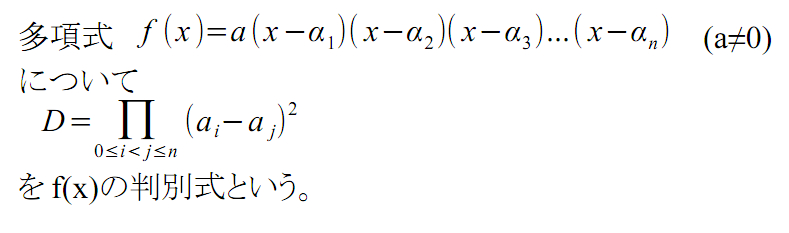
つまりどういうことかというと、
多項式f(x)の根 a1,a2,a3...an のうち2つを選びとった全て組み合わせの
差の平方をとり、それらを全部掛け合わせたものが判別式であるということです。
一つでも重複した根があればそれらの差の平方は0となって判別式全体も0となる、というわけです。
なぜ差を平方する必要があるかというと判別式を対称式にするためです。
そうすれば、同じく対称式である根と係数の関係(解と係数の関係)より
判別式が多項式の係数によって表せるようになるのです。
とりあえず、二次方程式を例にとって説明したいと思います。
二次方程式ax^2+bx+c=0 の2つの根をα,βとする。
判別式D=(α-β)^2
=(α+β)^2-4αβ
二次方程式の根と係数の関係より、
=(-b/a)^2-4c/a
=(b^2-4ac)/a^2
分子にお馴染みの二次方程式の判別式 b^2-4acが出てきました。
a^2は必ず0より大きい(a=0だと二次方程式にならない)ので
分子だけで重根の判定が可能です。
よって二次方程式の判別式D=b^2-4ac となるのです。
三次方程式についても、
ax^3+bx^2+cx+d=0 の3つの根をα,β,γとする
D=(α-β)^2(β-γ)^2(α-γ)^2
となり、計算していくと
=(b^2c^2+18abcd-4ac^3-4b^3d-27a^2d^2)/a^4
となる。aは必ず0より大きいので
D=b^2c^2+18abcd-4ac^3-4b^3d-27a^2d^2
非常に長い判別式です。しかし、三次方程式をいろいろ変形すると簡単になったりするのですが
話が長くなりすぎるし、僕もいまいち理解してないので興味があれば自分で調べて下さい。
まあ、何が言いたかったかというと判別式とは実は
多項式f(x)の根 a1,a2,a3...an のうち2つを選びとった全て組み合わせの
差の平方をとり、それらを全部掛け合わせた
という単純なものだということを紹介したかっただけです。
それだけ知ってもらえればOKです。
(続き)
ではここからが本題です。
判別式とはその多項式に重根(重複した根)が存在するかどうか確かめるための式です。
重根が存在すれば判別式は0となります。
つまりどういうことかというと、
多項式f(x)の根 a1,a2,a3...an のうち2つを選びとった全て組み合わせの
差の平方をとり、それらを全部掛け合わせたものが判別式であるということです。
一つでも重複した根があればそれらの差の平方は0となって判別式全体も0となる、というわけです。
なぜ差を平方する必要があるかというと判別式を対称式にするためです。
そうすれば、同じく対称式である根と係数の関係(解と係数の関係)より
判別式が多項式の係数によって表せるようになるのです。
とりあえず、二次方程式を例にとって説明したいと思います。
二次方程式ax^2+bx+c=0 の2つの根をα,βとする。
判別式D=(α-β)^2
=(α+β)^2-4αβ
二次方程式の根と係数の関係より、
=(-b/a)^2-4c/a
=(b^2-4ac)/a^2
分子にお馴染みの二次方程式の判別式 b^2-4acが出てきました。
a^2は必ず0より大きい(a=0だと二次方程式にならない)ので
分子だけで重根の判定が可能です。
よって二次方程式の判別式D=b^2-4ac となるのです。
三次方程式についても、
ax^3+bx^2+cx+d=0 の3つの根をα,β,γとする
D=(α-β)^2(β-γ)^2(α-γ)^2
となり、計算していくと
=(b^2c^2+18abcd-4ac^3-4b^3d-27a^2d^2)/a^4
となる。aは必ず0より大きいので
D=b^2c^2+18abcd-4ac^3-4b^3d-27a^2d^2
非常に長い判別式です。しかし、三次方程式をいろいろ変形すると簡単になったりするのですが
話が長くなりすぎるし、僕もいまいち理解してないので興味があれば自分で調べて下さい。
まあ、何が言いたかったかというと判別式とは実は
多項式f(x)の根 a1,a2,a3...an のうち2つを選びとった全て組み合わせの
差の平方をとり、それらを全部掛け合わせた
という単純なものだということを紹介したかっただけです。
それだけ知ってもらえればOKです。
PR
プロフィール
HN:
yorito
性別:
男性
職業:
高校生
自己紹介:
愛知県在住の高3男子が
心にうつりゆくよしなしごとを
そこはかとなく書き付けるブログです。
誰でもコメ歓迎。
心にうつりゆくよしなしごとを
そこはかとなく書き付けるブログです。
誰でもコメ歓迎。
カレンダー
カテゴリー
アクセスカウンター
ブログ内検索
NINJA TOOLS
雲野コア



 無題 by ショコラ
無題 by ショコラ 