アステロイドのおもちゃ！

旭苑の部紹介の放送部のスペースを見てみると去年までなかった部員紹介が書いているので拝見。

新３年生の欄を見てみるとS原君が「初の朗アナ系男子」と紹介されてました。
（※朗アナ・・・朗読・アナウンスのこと。放送部には朗アナと機材の２つの活動がある。）

朗アナ"系"ってなんなんだろう？S原君朗アナやってたっけ？

ってかそれ以前に僕、一年のとき朗アナやってたから僕が「初の朗アナ系男子」なはずなんだけど…

存在を忘れられたのか、なかったことにされたのか…。


まあ、それはおいといてクラスの食事会も終業式も終了し、放課後にマジアカやったりCD買ったりで

楽しく終わった２学年でした。のんびりと春休みを過ごしています。


…また話が変わりますが本当にのんびりしてると無為に過ごしてしまいそうなので

数学の話でもしますか。


この前クラスの頭脳、Mッキー君が悩んでいた問題が気にかかってて考えていました。

その問題は、

「長さ１の線分があり、その両端はそれぞれx軸、y軸上にある。

この線分が動く領域の境界線はアステロイドであることを示せ。」

という問題なのですがこの線分上の点をある文字で置くと四次式が出てきたり、

両端のx座標、y座標の二乗の和は１だから三角関数でおけるだろ！

と思っても上手いこと問題の答えに導くような式変形ができなかったりで解けませんでした。


諦めてネットで検索したらいい解法が見つかったので、

自分の言葉に直してまとめてみました。












…なんとなく分かるような分からないような証明ですね…。

tは0から1までの値を動くものだったのにdy/dxを求めることで具体的な値が出てきてしまってるし
（追記：cos^2θは0から1までを動くので問題無いです。
でも x=tcosθ y=(1-t)sinθ は領域を示す式だったのになぜアステロイドという曲線の式に？）

直線ABは常に境界線の接線となることはだいたい予想がつくのですが

そうではないときにこの解法は使えるのかと…。


いろいろ悩んでいたのですが包絡線というものを考えると上手く理解できると分かりました。

まあ、めんどくさいのでそれについての説明は割愛。

気になる場合は自分で調べておいて下さい。

ちなみに y=(-b/a)x+b を a=cosθ  b=sinθ と置いた式 y=(-tanθ)x+sinθ

のθの値をいろいろに変化させてグラフを書くとこうなります。












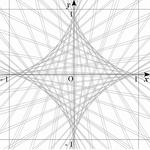
確かにアステロイドの形が残像として浮かび上がってきますね。


そんなこんなで今回も結構時間のかかった記事でした。

何か指摘や意見があれば。では。

2012/03/21 (Wed) 数学 Comment(0)