実数の穴を埋める"超実数"

この前の「∞は実数か？」の記事で

∞をどんな実数よりも大きくなりうる数、実直線の外側にある数と捉え、

厳密にいって∞は実数ではないとしました。

しかし、実数ではないなら一体何なのでしょう？

数Ⅲの内容で実数ではない∞を普通に使っちゃってますが本当にいいのでしょうか？


ここで、実数について考えなおしてみます。

実数は確かに実直線の上に乗っている数として一次元的に捉えることができますが

実数一つ一つはあくまで点、つまりゼロ次元的です。

直線の上に点が乗っかっているわけですが、直線は直線、点は点であって

いくら点が集まったところでそれは点の集まりに過ぎないわけです。


そこで実直線の穴を埋めるために定義された数があります。

超実数という数です。

この超実数という数には

無限小超実数、無限大超実数、有限超実数の三種類があります。

[つづきはこちら]

2012/04/15 (Sun) 数学 Comment(0)

∞は実数か？

数Ⅲの教科書より登場する∞という概念。

この用語を使う文脈にもよりますが

「無限に大きい数」、言い換えれば

∞という数は数直線上の正の方向の遥か彼方にあるという認識を持っているのが普通かもしれません。

数直線上にあるということはその数は少なくとも実数であるということです。

しかし、∞は本当に実数でしょうか？


実数全体の集合を"R"と表すことがあります。

他にも有理数の集合は"Q"、整数は"Z"、自然数は"N"などと慣習的に表記します。

自然数の集合Nの要素は1,2,100,5282,5兆,1無量大数などいくらでもあげられるでしょう。

他の集合も言わずもがなです。

当たり前すぎるかもしれませんが自分でそれぞれの集合について適当な要素をあげてみると、

例えそれがどんな大きな数であってもある定まった数、有限な数であることに気づきませんか？

そうなのです。これらの集合のうちどんな要素をあげたとしても

必ずそれより大きい要素がその集合の中に見つからないといけないのです。


"∞"は定義からしてどんな実数よりも大きい"数"といえるかもしれませんが

それはつまり、「∞より大きい実数は存在しない」とも言い換えられませんか？


ですので ∞ ∉ R としたほうがいいようです。


例えば、2以上の区間を表すときに [2,∞) と表記しますね。

[2,∞] ではダメなのかと疑問に思ったことはありませんか？

これは"∞"という要素が実数の集合の中に含まれないからです。

∞の側を閉じてしまうとそれも実数の数直線（実直線）上に存在するということになってしまいます。


"∞"とは「どんな実数よりも大きくなりうる数」や「実直線の外側にある数」との認識を持ったほうが

正確かもしれませんね。

2012/03/28 (Wed) 数学 Comment(2)

前回の記事の補足とか

前回、ある命題A,Bを用いて

"A ⇒ B" という命題が定義され、

それが "￢A∨B" という命題の真偽と一致することを説明しました。

真偽が一致する、いわば2つの命題が同値（論理同値）であることを

"P ≡ Q" や "P ⇔ Q" などといった記号で表します。

つまり "A ⇒ B ≡ ￢A∨B"・・・① と書けるわけです。

この関係を覚えるためのいい例文があったので紹介します。それは、

「動いたら殺すぞ！」

「動くな、さもないと殺すぞ！」

この２つです。どちらも同じ事を言ってますよね？

「動く」という動作をAとし、「殺す」という動作をBとします。

すると、

「AするならばBするぞ！」・・・"A ⇒ B"

「Aするな（￢A）、さもないと（∨）Bするぞ！」・・・"￢A∨B"

①の関係と一致しますね。


ただ、この覚え方はうちの学校の生徒にとってはあの事件を彷彿とさせるとして不評だという噂です（


もう一つ補足というか自分が考えたことについてなんですが

[つづきはこちら]

2012/03/24 (Sat) 数学 Comment(0)

「1=2ならば1+1=2である」は真か偽か？

論理について勉強していたのですが

自分でなんとか噛み砕いて理解したものを忘れないためにも、

みなさんにも理解しやすいようにここに書き留めておきます。

今回は論理についてのお話です。


論理というと高校数学の最初のほうに習った記憶があると思います。

いわば数学の基本、土台とも言えますが

人によって結構得意不得意の分かれるところだと思います。


ではみなさんは記事タイトルの命題に答えられるでしょうか？


1=2！？ その時点でおかしい…

仮に1に2を代入すると2+2=4、でもは1+2とも置けるし…

そもそも1=2としておいてそんな計算意味あるんでしょうか？


ではちょっと話を逸らして、数Aでこんな記号習いましたよね？

"p ⇒ q"…「pならばqである」

一般に正しいか正しくないかが定まる文や式を命題と言いました。

それが正しければ命題は「真」、正しくなければ「偽」といいますね。

例えば「アンパンならばパンである」これは間違いなく真です。

「x>2ならばx^2>4である」これも真。

ではこれは？「x,yがともに無理数ならばx+yは無理数である」

これは偽です。反例をあげると(1-√2)+(1+√2)=2 とかね。


これらの命題を見て何か共通点はありませんかね？

考えてみて下さい。

[つづきはこちら]

2012/03/23 (Fri) 数学 Comment(3)

アステロイドのおもちゃ！

旭苑の部紹介の放送部のスペースを見てみると去年までなかった部員紹介が書いているので拝見。

新３年生の欄を見てみるとS原君が「初の朗アナ系男子」と紹介されてました。
（※朗アナ・・・朗読・アナウンスのこと。放送部には朗アナと機材の２つの活動がある。）

朗アナ"系"ってなんなんだろう？S原君朗アナやってたっけ？

ってかそれ以前に僕、一年のとき朗アナやってたから僕が「初の朗アナ系男子」なはずなんだけど…

存在を忘れられたのか、なかったことにされたのか…。


まあ、それはおいといてクラスの食事会も終業式も終了し、放課後にマジアカやったりCD買ったりで

楽しく終わった２学年でした。のんびりと春休みを過ごしています。


…また話が変わりますが本当にのんびりしてると無為に過ごしてしまいそうなので

数学の話でもしますか。


この前クラスの頭脳、Mッキー君が悩んでいた問題が気にかかってて考えていました。

その問題は、

「長さ１の線分があり、その両端はそれぞれx軸、y軸上にある。

この線分が動く領域の境界線はアステロイドであることを示せ。」

という問題なのですがこの線分上の点をある文字で置くと四次式が出てきたり、

両端のx座標、y座標の二乗の和は１だから三角関数でおけるだろ！

と思っても上手いこと問題の答えに導くような式変形ができなかったりで解けませんでした。


諦めてネットで検索したらいい解法が見つかったので、

自分の言葉に直してまとめてみました。












…なんとなく分かるような分からないような証明ですね…。

tは0から1までの値を動くものだったのにdy/dxを求めることで具体的な値が出てきてしまってるし
（追記：cos^2θは0から1までを動くので問題無いです。
でも x=tcosθ y=(1-t)sinθ は領域を示す式だったのになぜアステロイドという曲線の式に？）

直線ABは常に境界線の接線となることはだいたい予想がつくのですが

そうではないときにこの解法は使えるのかと…。


いろいろ悩んでいたのですが包絡線というものを考えると上手く理解できると分かりました。

まあ、めんどくさいのでそれについての説明は割愛。

気になる場合は自分で調べておいて下さい。

ちなみに y=(-b/a)x+b を a=cosθ  b=sinθ と置いた式 y=(-tanθ)x+sinθ

のθの値をいろいろに変化させてグラフを書くとこうなります。












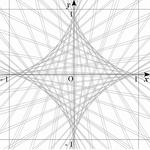
確かにアステロイドの形が残像として浮かび上がってきますね。


そんなこんなで今回も結構時間のかかった記事でした。

何か指摘や意見があれば。では。

2012/03/21 (Wed) 数学 Comment(0)