判別式とは

みなさん判別式というと二次方程式の判別式D=b^2-4acをまず思い浮かべると思います。

でもこれを解の公式から導き出すことを学校で教えられ、なんとなく使っている人も多いでしょう。

今回は判別式についてお話しします。

ではまず説明に使う用語と記号について紹介します。

めんどうな場合は読み飛ばして（続き）に飛んで下さい。

一つ目は「根」について








「解」によく似てますね。でも解とは少し違います。

「解」とはあくまでf(x)=0を満たすxの値のことです。

同じものが２つあればそれをまとめて一つとして考えます。

例えば、(x-1)^2=0の「解」は一つですが「根」は２つと考えます。

でも今回は、同じものだとして「解」と読みかえてもらっても構いません。


２つ目に総乗記号についてです。総乗記号Πは次のように定義されます。








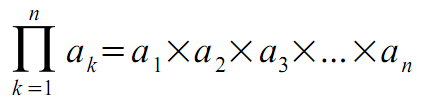
要するにΣ（シグマ）の掛け算バージョンと思えばすぐ理解できるでしょう。

 

[つづきはこちら]

2012/03/14 (Wed) 数学 Comment(2)

双曲線関数を使った、積分の実験的解法

昨日、双曲線関数の性質を利用してなんとか積分に応用できないかと

3～4時間考えていたのですが

なんだか特殊な解法を思いついたのでその成果をここに記します。

例にあげる問はこの前の授業で出てきた、

y=x^2においてxが0から1までの曲線の長さの問題です。

数式エディタの使い方まで覚えて作ったので心して読んでもらいたいです。












どうでしょうか？

こんな簡単な答えにならなかったような気がするので

なんか間違っている気がしますが。

αの求め方とか個人的にうまくできたと思うのですけど。


これ作るのにめちゃめちゃ時間かかりました…。

他にもいろいろ書いておきたい成果はあるのですが

それを書くには余白が狭すぎる時間がかかりすぎるので

こんなもんにしておきます。


なにか指摘や意見があればお願いします。

2012/03/12 (Mon) 数学 Comment(3)

i^i

今日放課後の数研の活動で

任意の複素数の極形式表示 z=|z|e^iθ から

i^i=e^(-π/2) という結論を出しましたが

よく考えたら極形式って極座標と同じで偏角が2π回転したら一周して同じ値になるじゃん…


つまりもう少し極形式を一般的に書くと z=|z|e^i(θ+2nπ) ・・・☆ となるわけです。
（ただしnは任意の整数）

しかし普通の複素数ならばオイラーの公式より cosθ+isinθ っていう三角関数の和の形に直せるから

2nπがあろうとなかろうと結局同じ値になるのですが

i^i=e^(-π/2) という具体的な指数で表された実数値が出てきてる以上は

2nπのあるなしで大きな違いが出てきます。

もう一度☆を使ってi^iを考えなおしてみると

i=|i|e^i(π/2+2nπ)

よって

i^i=e^(-π/2-2nπ)

nは任意の整数のため2nπの符号を変えても一般性を失わないので

i^i=e^(-π/2+2nπ)

こうなりますね。

そう考えるとi^iに対応する実数は一つじゃないどころか無限個存在することになるわけです！

もし間違ってたら指摘をお願いしたい。


やけに丁寧に書いてみましたが

S井先生みたいに逆に分かりづらくなってないかな…？


こんな記事を書くのも楽しいものですね。

読んでる人は楽しくないかもしれないけど。。

2012/03/02 (Fri) 数学 Comment(2)